Bonnet transformation D –> G –> P

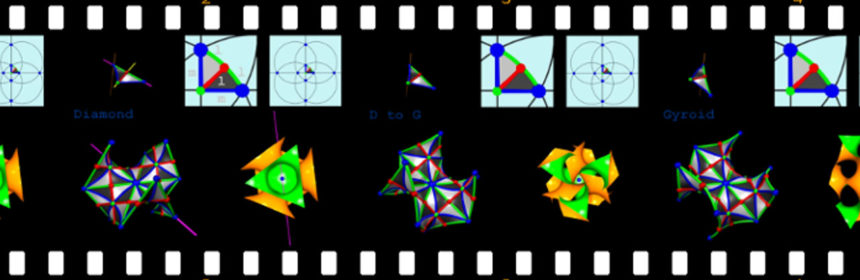
The three cubic triply-periodic minimal Diamond, Gyroid and Primitive surfaces are related to each other by the so-called Bonnet transformation. That means they are specific members of a single one-parameter family of surfaces, called the Bonnet family with free parameter t for the specific values t=0 (Diamond), t~38^o (Gyroid) and t=90^o (Primitive). However, in contrast to the D, G and P surfaces, all other members of that family have self-intersections. The animation shows the transformation of a single asymetric patch in E³ (top left), of an extended patch where the coloring of the asymmetric patch has been retained and also showing the three-fold rotation axis common to all members (bottom left) and of a large enough patch of the surface that illustrates the self-intersections (bottom right). In that last image one side of the surface is orange, and the other green. Also shown are the tiles of the complex plane that (via the Weierstrass equation) give rise to the asymmetric unit patch.

Animation file: (40MB MPG)