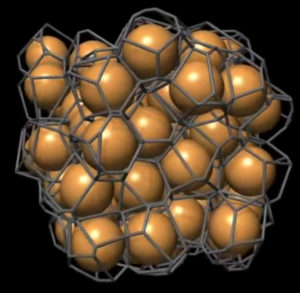
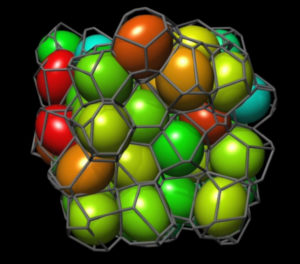
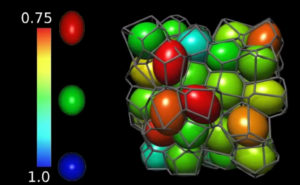
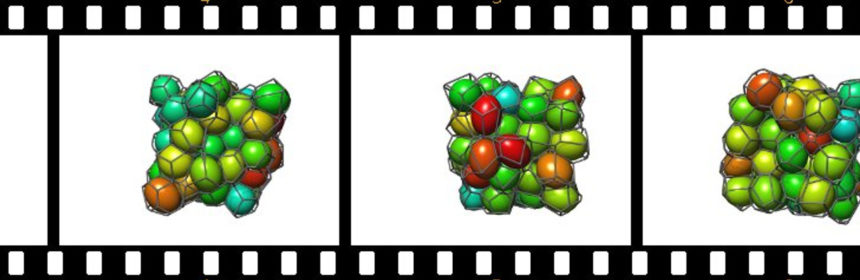
Animation of anisotropic Voronoi cells of an isotropic sphere packing
Investigating how tightly objects pack space is a long-standing problem, with relevance for many disciplines from discrete mathematics to the theory of glasses. Here we report on the fundamental yet so far overlooked geometric property that disordered mono-disperse spherical bead packs have significant local structural anisotropy manifest in the shape of the free space associated with each bead.
Jammed disordered packings from several types of experiments and simulations reveal very similar values of the cell anisotropy, showing a linear decrease with packing fraction. Strong deviations from this trend are observed for unjammed configurations and for partially crystalline packings above 64%. These findings suggest an inherent geometrical reason why, in disordered packings, anisotropic shapes can fill space more efficiently than spheres, and have implications for packing effects in non-spherical liquid crystals, foams and structural glasses. See details in
- Schröder-Turk et al, Disordered spherical bead packs are anisotropic , Europhys Lett 90(3), 34001 (2010)
The animations show a subset of a jammed disordered packing of beads in 3D with the corresponding Voronoi diagram (brown beads). The second set of animations show the same subset of the Voronoi diagram as shown in animation 1, however with the beads replaced by ellipsoids that match the anisotropy (measured by the min/max eigenvalue ratio of the Minkowski tensor W020, and orientation of the Voronoi cells.
This animation is from 2010, so quite old. Simon Weis has produced a nicer newer version of a similar visualisation, but with improved graphics and with a pretty funky 3D headset. Check it out appendix 2 of his thesis (click this link)
Acknowledgments: Position data for the beads displayed in this animation was collected by X-ray tomography by Tomaso Aste, Tim Senden and Mohammad Saadatfar (ANU). See publication Aste et al, An invariant distribution in static granular media , Europhys Lett 79, 24003 (2007).
Click on the images below for animation files
(animation of original spherical particles)
(anisotropy-matched ellipsoids without scale bar)
(anisotropy-matched ellipsoids with scale bar)
(This post is, in large parts, a copy of my post on my earlier web page. Hence, the publication date has been reset to 2015)