Self-assembled tri-continuous phases : like a double gyroid with three network channels

The bicontinuous phases, composed of two interthreaded channels separated by a matrix domain have a firm place in soft matter self-assembly, from lipids to copolymers. This post high-lights some of our recent work that shows that more complicated geometries, with three rather than two channel domains, may also result from self-assembly.

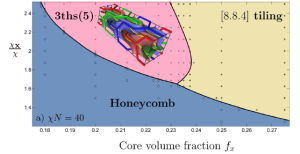
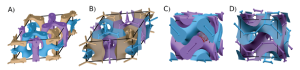
In a recent paper (Fischer et al, Macromolecules 47, 7424-7430, 2014) we have looked at how star-copolymers consisting of three immiscible arms can be coaxed into forming tricontinuous geometries. What we found was that the introduction of a molecular core helps to destabilise the hexagonal honeycomb phase in favour of tricontinuous geometries. We have used spectral self-consistent field theory to show that a tricontinuous structure with monoclinic symmetry, called 3ths(5), based on the intergrowth of three distorted ths nets, is an equilibrium phase of triblock star-copolymer melts when an extended molecular core is introduced. The introduction of the core enhances the role of chain stretching by enforcing larger structural length scales, thus destabilizing the hexagonal columnar phase in favor of morphologies with less packing frustration. This study further demonstrates that the introduction of molecular cores is a general concept for tuning the relative importance of entropic and enthalpic free energy contributions, hence providing a tool to stabilize an extended repertoire of self-assembled nanostructured materials.

In a short comment (Fischer et al, Soft Matter 11, 1226-1227, 2015) , we discuss the emergence of a different triple-network phase in gemini surfactants (Sorenson et al, Soft Matter 10, 8229-8235, 2014) and as a mesoporous silicate (Han et al, Nature Chem 1, 123 – 127, 2009) in terms of geometric chain stretching and bending free energies. We demonstrate by SCFT that even in simple diblock copolymers this geometry, based on the intergrowth of so-called etc nets, this geometry almost represents a stable phase: While it is not a minimum of the free energy functional, the free energy penalty of this 3-etc phase compared to cylindrical and gyroid phases is small, in the parameter space near the hexagonal to gyroid transition.

The idea of tri- or polycontinuous space partitions is not brand new, but had been canvassed in quite a few earlier papers, including Hyde & Oguey (Eur. Phys. J. B 2000, 16, 613−630), Hyde & Ramsden (Europhys. Lett. 2000, 50, 135−141), Hyde et al (J. Solid State Sci. 2003, 5, 35−45), Hyde & Schröder (Curr. Opin. Colloid Interface Sci. 2003, 8, 5−14) and Schröder-Turk et al (Faraday Discuss. 2013, 161, 215−247).

We thank Mohammad Saadatfar for 3D-printing of the 3ths(5) sculpture and Andreas Döring for the photography.

We thank Mohammad Saadatfar for 3D-printing of the 3ths(5) sculpture and Andreas Döring for the photography.