Snow Flakes on Kelvin’s polyhedra: Thomas Pigeon’s artistic take on the 8-fold Gyroid topology
Congratulations to Thomas Pigeon on completing a lovely animation of the 8-srs structure, the 8-fold highly symmetric intergrowth of 8 equal-handed gyroid graphs. Thomas came to Murdoch University for a project in 2017, and self-taught himself the mastery of houdini. Thomas, thanks for sharing your beautiful animation:
The 8-srs is the composition of 8 intergrown equal-handed gyroid nets, in a highly symmetric fashion with cubic symmetry, first described in these works
- S.T. Hyde & C. Oguey, “From 2D hyperbolic forests to 3D Euclidean entangled thickets“, Eur. Phys. J. B 16, 613-630 (2000)
- S.T. Hyde & S. Ramsden, “Polycontinuous morphologies and interwoven helical networks“, Europhys. Lett., 50 (2), pp. 135-141 (2000)
Thomas’ animation is inspired by a construction that relates to Kelvin polyhedra, fourteen-sided polyhedra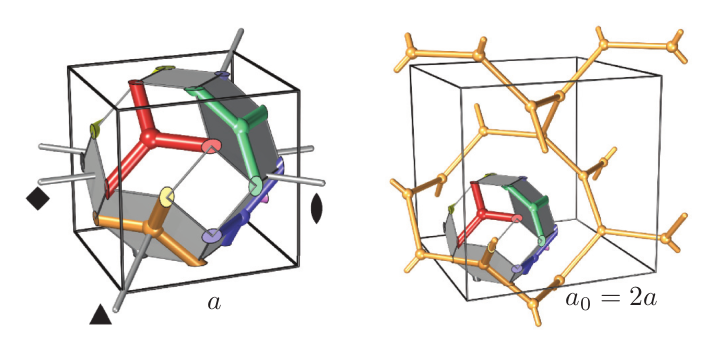 
with 6 squares and 8 hexagons the packing of which Kelvin at the time thought might relate to the structure of the ether. When one decorates one of the hexagons of this polyhedra with a star and arranges the polyhedra in a symmetric fashion, the Gyroid graph results. When one decorates all of the hexagons with a star, the 8-srs can emerge. This idea has been described in this paper
- M.E. Evans, V. Robins & S.T. Hyde, “Periodic entanglement I: networks from hyperbolic reticulations“, Acta Cryst A 69, 241 (2013)
The 8-srs has some remarkable optical properties: Despite being very chiral, it shows no sign of circular dichroism but very large optical rotary power. The optical properties of the 8-srs have been elucidated by Matthias Saba through group theory and by Ben Cummings and Min Gu and their students through nanofabricationi experiments and simulations:
- Saba et al, “Group theory of circular-polarization effects in chiral photonic crystals with four-fold rotation axes applied to the eight-fold intergrowth of gyroid nets“,Phys. Rev. B 88, 245116 (2013)
- F. Turella, B. Cumming, G.E. Schröder-Turk, M. Gu, “Observation of optical activity in dielectric biomimetic 8-srs networks“, Optics Letters 40, 4795-4798 (2015)
- M. Saba, M.D. Turner, M. Gu, K. Mecke, and G.E. Schröder-Turk, “Chiral Photonic Crystals with 4-fold Symmetry: Band Structure and S-Parameters of Eight-Fold Intergrown Gyroid Nets”, Proceedings of SPIE Vol 8923, 89233T-1 (2013)
On a side note, Thomas Pigeon proved himself a very competent player of the thong-a-phone. Here’s some evidence for it:
… and with additional support from Max Scharf and Duncan Farrow: