When mixed with oranges, pears prefer Diamonds….
… over Gyroids. Philipp Schönhöfer has completed a nice piece of work to extend on the pear-shaped particle simulations that we have been doing in collaboration with Doug Cleaver and Matthieu Marechal. Previously we had simulated a system of nearly hard pear-shaped particles and found that they form the Gyroid geometry. Now, it turns out that the addition of a small number of spherical particles leads to the formation of the double diamond phase, at least in relatively small simulation boxes.
This work has been published in the following article
- P.A. Schönhöfer, D. Cleaver and G.E. Schröder-Turk, “Double diamond phase in pear-shaped nanoparticle systems with hard sphere solvent“, Journal of Physics D: Applied Physics 51(46), 464003 (2018)
which is a paper in a special issue on “Collective Behaviour of Living Matter”, organised by Ben Fabry, Daniel Zitterbart and Robert Endres. I am grateful to Ben Fabry who invited and encouraged me to submit an article for this issue.
The abstract of the article reads: “The mechanisms behind the formation of bicontinuous nanogeometries, in particular in vivo, remain intriguing. Of particular interest are the many systems where more than one type or symmetry occurs, such as the Schwarz’ diamond surface and Schoen’s gyroid surface; a current example are the butterfly nanostructures often based on the gyroid, and the beetle nanostructures often based on the diamond surface. Here, we present a computational study of self-assembly of the bicontinuous Pn
m diamond phase in an equilibrium ensemble of pear-shaped particles when a small amount of a hard-sphere ‘solvent’ is added. Our results are based on previous work that showed the emergence of the gyroid Ia
d phase in a pure system of pear-shaped particles (Schönhöfer et al 2017 Interface Focus 7 20160161), in which the pear-shaped particles form an interdigitating bilayer reminiscent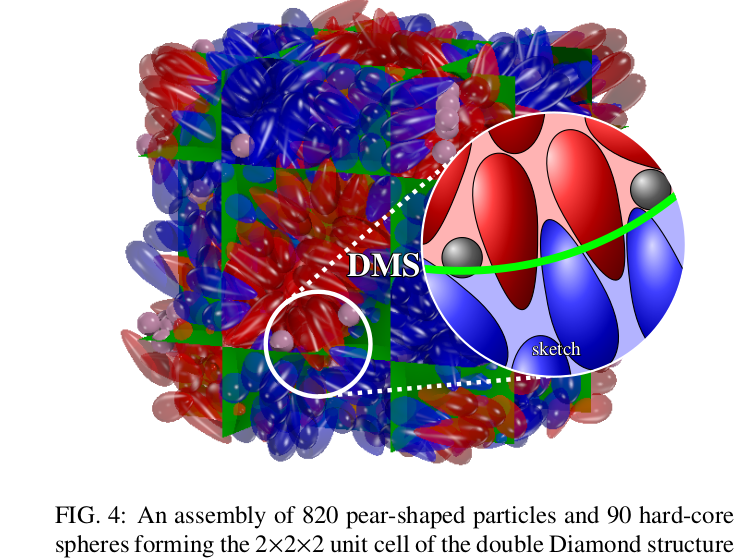 
of a warped smectic structure. We here show that the addition of a small amount of hard spherical particles tends to drive the system towards the bicontinuous Pn
m double diamond phase, based on Schwarz diamond minimal surface. This result is consistent with the higher degree of spatial heterogeneity of the diamond minimal surface as compared to the gyroid minimal surface, with the hard-sphere ‘solvent’ acting as an agent to relieve packing frustration. However, the mechanism by which this relief is achieved is contrary to the corresponding mechanism in copolymeric systems; the spherical solvent tends to aggregate within the matrix phase, near the minimal surface, rather than within the labyrinthine channels. While it may relate to the specific form of the potential used to approximate the particle shape, this mechanism hints at an alternative way for particle systems to both release packing frustration and satisfy geometrical restrictions in double diamond configurations. Interestingly, the lattice parameters of the gyroid and the diamond phase appear to be commensurate with those of the isometric Bonnet transform.”
There are some peculiarities and sensitivities about the potential that we are currently working on. Stay tuned for an update.
See also these articles on related systems:
- P.A. Schönhöfer, G.E. Schröder-Turk, M. Marechal, “Density functional theory for hard uniaxial particles: Complex ordering of pear-shaped and spheroidal particles near a substrate“, The Journal of Chemical Physics 148, 124104 (2018)
- Philipp W. A. Schönhöfer, Laurence J. Ellison, Matthieu Marechal, Douglas J. Cleaver, and Gerd E. Schröder-Turk, “Purely Entropic Self-Assembly of the Bicontinuous Ia3d Gyroid-Phase“, Interface Focus 7(3), 20160161 (2017)
A very big thank you to Goran Ungar, for interest in the Diamond formation, for advice on Diamond forming systems … and for sending me the image of the beer coaster advertising double diamond ales.