The magic of Lloyd’s algorithm: Universal hidden order in amorphous cellular geometries

Animation file: (Nature Comms Suppl Info page)

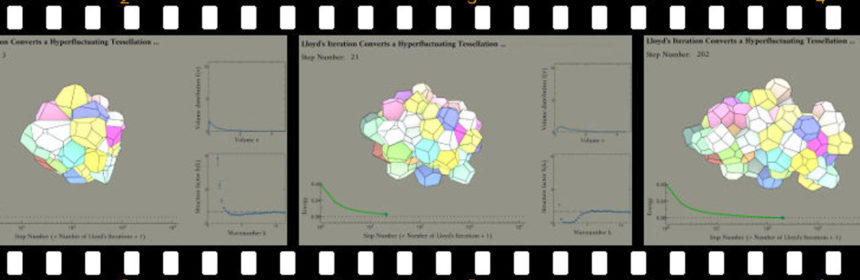
Lloyd’s algorithm, described by Lloyd in the journal IEEE Trans. Inf. Theory (vol 28, pages 129) is an iteration that’s by now more than 30 years old and with a long history of applications. Yet, its application to 3D disordered point patterns reveals a new interesting aspect of it: a seeming convergence to a very robust disordered state which shows virtually no memory of the disordered configurations it started from (universal) and which is characterised by very low fluctuations of density (effectively hyperuniform). We have published this in

• M.A. Klatt, J. Lovric, D. Chen, S.C. Kapfer, F.M. Schaller, P.W.A. Schönhöfer, B.S. Gardiner, A.-S. Smith, G.E. Schröder-Turk, S. Torquato, “Universal hidden order in amorphous cellular geometries“, Nature Communications 10, 811 (2019)

Here’s the abstract of our paper: Partitioning space into cells with certain extreme geometrical properties is a central problem in many fields of science and technology. Here we investigate the Quantizer problem, defined as the optimisation of the moment of inertia of Voronoi cells, i.e., similarly-sized ‘sphere-like’ polyhedra that tile space are preferred. We employ Lloyd’s centroidal Voronoi diagram algorithm to solve this problem and find that it converges to disordered states associated with deep local minima. These states are universal in the sense that their structure factors are characterised by a complete independence of a wide class of initial conditions they evolved from. They moreover exhibit an anomalous suppression of long-wavelength density fluctuations and quickly become effectively hyperuniform. Our findings warrant the search for novel amorphous hyperuniform phases and cellular materials with unique physical properties.