Author: Gerd Schroeder-Turk

Voxelised Minimal Surface Structures (from Kapfer et al, Biomaterials 2011)

These are the voxelised datasets that were used for FEM calculations of effective elastic properties and for Lattice Boltzmann calculations of permeabilities in our article

  • S.C. Kapfer, S.T. Hyde, K. Mecke, C.H. Arns, and G.E. Schröder-Turk, “Minimal surface scaffold designs for tissue engineering”, Biomaterials 32(29), 6875-6882 (2011)

(Click here for Sebastian Kapfer’s page for voxelised data sets)

These data sets were used to obtain the following result which even now (in 2019) I consider quite amazing: “As the key result of this article, we have shown that, at the same solid volume fraction, sheet solids have a subs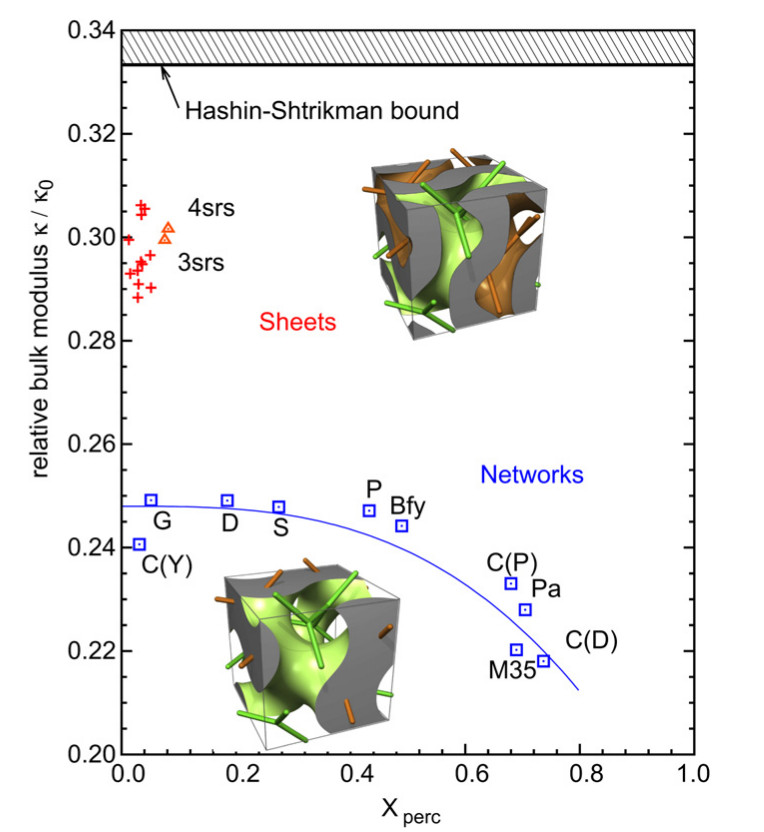biomaterials-sheet-solids-versus-network-solids-elastic-propstantially higher effective bulk modulus k and direction-averaged Young’s modulus E than network solids, for a wide range of volume fractions and material parameters. While a comprehensive explanation of this behavior is elusive, it can be compared to the differences between hollow steel pipes and solid steel struts with respect to bending rigidity. In civil engineering, it is a well-known fact that at equal material usage, a hollow cylinder is preferrable to a solid cylindrical strut; the moment of inertia of the beam cross-section enters the bending rigidity. Minimal surface sheets act as the triply-periodic analogon of the hollow pipe, whereas network solids are representing networks of solid cylindrical struts.”

Bonnet transformation D –> G –> P

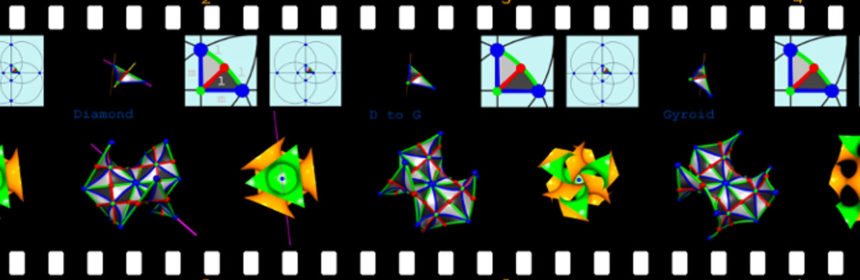
The three cubic triply-periodic minimal Diamond, Gyroid and Primitive surfaces are related to each other by the so-called Bonnet transformation. That means they are specific members of a single one-parameter family of surfaces, called the Bonnet family with free parameter t for the specific values t=0 (Diamond), t~38o (Gyroid) and t=90o (Primitive). However, in contrast to the D, G and P surfaces, all other members of that family have self-intersections. The animation shows the transformation of a single asymetric patch in E3 (top left), of an extended patch where the coloring of the asymmetric patch has been retained and also showing the three-fold rotation axis common to all members (bottom left) and of a large enough patch of the surface that illustrates the self-intersections (bottom right). In that last image one side of the surface is orange, and the other green. Also shown are the tiles of the complex plane that (via the Weierstrass equation) give rise to the asymmetric unit patch.

Animation file: (40MB MPG)

1 … 5 6 7