“More is different”: Nanofabricated chiro-optical material based on 8-fold intergrowth of gyroid

In a totally different context to the original quote and article, Phil Anderson’s quote “More is different” holds also for the chiro-optical response of gyroid-based photonic materials. Eight intergrown Gyroids give a substantially different chiro-optical response than the single gyroid. The group theoretic prediction from Matthias Saba’s PhD work (Saba et al, PRB 2013) has now been experimentally validated by Nanofabrication experiments in the Center for Microphotonics at Swinburne University (Turella et al, Optics Letters, 2015). Read more

In a Material World

“In a Material World: Hyperbolic Geometry in Biological Materials”, by Myf Evans and myself, is a popular-science type essay on the sort of geometric questions that we see of relevance for soft matter physics, materials science, biology, etc. In particular, what’s the role of hyperbolic geometry and triply-periodic minimal surfaces, and what’s the geometric rationale why they form in soft matter self-assembly. Hopefully an entertaining read, with no claim to be comprehensive, and certainly not original research. Read more

Conference Geometry and Physics of Random Spatial Structures, Black Forest 7-11 Sept 2015

Held in the picturesque Black Forest region of Germany from 7-11 September 2015, this conference will cover the mathematics and physics of disordered spatial structures and systems. Keynote speakers at this event include: Anton Bovier, Paul Chaikin, Wiebke Drenckhan, Matthew Kahle, Randall Kamien, Domenico Marinucci, Frank den Hollander and Rien van der Weygaert. We’re still accepting poster abstracts for this conference, see www.gpsrs.de

Shape Up 2015 : Exercises in Materials Geometry and Topology

We’re still accepting abstracts for what shapes up to be an exciting international conference  on real-world materials, dead and alive, with complex spatial microstructures. An interdisciplinary discussion meeting on patterns and geometry, and their role in biological and synthetic microstructured materials and tissue. We invite contributions from biology, chemistry, materials science, mathematics, physics and related fields addressing the genesis, properties and function of complex nano-scale geometries, as well as underlying geometric and topological concepts for the study of complex structure and shape. More information can be found on www.shape-up.academy. See you in Berlin! Read more

Propagation of cell-level stress contributions in sheared random foams (by Myf Evans)

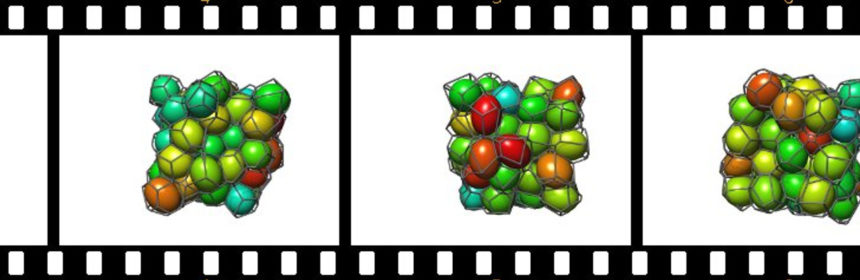
The evolution of the spatial structure of foams, during mechanical shear but also during diffusive coarsening, occurs by continuous geometric deformations maintaining cell topology interspersed with sudden topological transitions when cells change neighborhood. Following a topological transition, the foam undergoes significant and large-scale geometric deformations. This animation shows an animation of the Surface Evolver simulations of sheared foams, used as the basis of the analysis in Evans et al, PRL 111, 138301 (2013).

Animation with Plateau borders: (mp4)

Animation without Plateau borders: (mov)

We have used these simulation techniques to study the stress propagation in foams, as published in Evans et al: Quasistatic simple shearing flow of random monodisperse soap froth is investigated by analyzing surface evolver simulations of spatially periodic foams. Elastic-plastic behavior is caused by irreversible topological rearrangements (T1s) that occur when Plateau’s laws are violated; the first T1 determines the elastic limit and frequent T1 avalanches sustain the yield-stress plateau at large strains. The stress and shape anisotropy of individual cells is quantified by Q, a scalar derived from an interface tensor that gauges the cell’s contribution to the global stress. During each T1 avalanche, the connected set of cells with decreasing Q, called the stress release domain, is networklike and nonlocal. Geometrically, the networklike nature of the stress release domains is corroborated through morphological analysis using the Euler characteristic. The stress release domain is distinctly different from the set of cells that change topology during a T1 avalanche. Our results highlight the connection between the unique rheological behavior of foams and the complex large-scale cooperative rearrangements of foam cells that accompany distinctly local topological transitions. (this is the abstract of Evans et al)

Publications:
Evans et al, Networklike Propagation of Cell-Level Stress in Sheared Random Foams , Phys Rev Lett 111, 138301 (2013)

Authorship:

This animation was produced by Myfanwy Evans, from Surface Evolver data produced in cooperation with Andrew Kraynik.

Erpel : Sebastian Kapfer’s FEM code for effective elastic properties of voxelised spatial structures

Erpel is a finite-element code computing effective elastic properties of anisotropic multiphase media. It implements a conjugate-gradient scheme on cubic voxels and has been proven to scale to at 768³ voxels in aErpel_image_small MPI environment. Developed by Sebastian Kapfer, partially while spending some time in the Applied Maths group at the Australian National University.

Main page for information is Sebastian’s page, click here erpel page. (PDF of Erpel page).

This code was used in the following scientific journal publications Biomaterials 2011, Langmuir 2011, Adv Mater 2011

Code is at github: https://github.com/skapfer/erpel

 

Animation of anisotropic Voronoi cells of an isotropic sphere packing

Investigating how tightly objects pack space is a long-standing problem, with relevance for many disciplines from discrete mathematics to the theory of glasses. Here we report on the fundamental yet so far overlooked geometric property that disordered mono-disperse spherical bead packs have significant local structural anisotropy manifest in the shape of the free space associated with each bead.

Read more

1 … 4 5 6 7